Fluxos líquidos e brutos

Suponha que acompanhamos uma população de 1 000 indivíduos em dois anos. No ano 1, haviam 200 indivíduos em situação de pobreza. No ano 2, foram encontradas 300 pessoas em situação de pobreza. Podemos dizer que 100 pessoas entraram em situação de pobreza?

A resposta é não! De fato, a diferença líquida no total de pessoas pobres é 100. Entretanto, pode ser que as 300 pessoas do ano 2 não estejam entre as 200 do período 1. Então, 100 é um fluxo líquido: a diferença entre as pessoas que entraram e as pessoas que saíram da pobreza entre os períodos. Por sua vez, as entradas e saídas são fluxos brutos.

Isso pode parecer intuitivo, mas é um erro comum. Por exemplo, esta notícia diz que “23,3 milhões de brasileiros entraram em situação de vulnerabilidade social”. Este não é o número de pessoas que entraram em situação de pobreza, mas o saldo das pessoas em situação de pobreza.

Em geral, esta diferenciação é um preciosismo de economistas ou estatísticos. Mas os fluxos brutos podem mostrar que a pobreza é uma situação instável, com muitas pessoas saindo e entrando na pobreza entre dois períodos.

Estimando fluxos brutos com não-resposta

Se temos uma amostra que acompanha os mesmos indivíduos em dois períodos, podemos estimar os fluxos. A princípio, com resposta completa, isso não é um grande problema: seria o mesmo que fazer uma tabela de contingência com a mesma variável medida em momentos distintos.

Porém, na prática, as coisas são um pouco mais complicadas. Quando coletamos os dados, é possível que pessoas se recusem a participar da entrevista. E, em muitos casos, essa recusa em responder pode enviesar os resultados.

Stasny (1987) desenvolve um método para obter estimativas de fluxos brutos com não-resposta diferencial. Alguns anos mais tarde, Rojas, Trujillo e Silva (2014) mostram como aplicar esta metodologia usando planos amostrais complexos. nos dois casos, a aplicação envolve estimação de fluxos ocupacionais — i.e., quem perdeu emprego, quem saiu do desemprego, etc.

Mas o que isso tem a ver com epidemia?

Fluxos brutos em modelos epidemiológicos

Em epidemiologia, um dos assuntos que considero mais interessantes são os modelos compartimentais. No nosso exemplo, vamos manter a estrutura mais simples, o Modelo SIR. Nele, existem três estados de saúde:

• Susceptible: pessoas suscetíveis à doença;
• Infectious: pessoas doentes, com potencial de transmissão;
• Recovered: pessoas que se recuperaram da doença e estão imunes.

Podemos vê-lo como uma cadeia de Markov: dada uma distribuição inicial, é possível prever a distribuição no período seguinte. As probabilidades de transição entre estas categorias são, basicamente, probabilidades condicionais em relação à categoria inicial. Com esta matriz de probabilidades de transição, é possível ter informações muito importantes, como a velocidade da epidemia. O vídeo abaixo tem uma explicação mais detalhada destes conceitos:

Certo, mas como isso funcionaria na prática?

Simulação

Considere uma população de tamanho \(N = 10^5\) indivíduos, seguindo um modelo multinomial com as seguintes probabilidades iniciais dos estados SIR:

\[ \eta = \begin{pmatrix} .85 & .10 & .05 \end{pmatrix} \]

Entre o período 1 e 2, a população está sujeita às seguintes probabilidades de transição:

\[ P = \begin{pmatrix} p_{ij} \end{pmatrix} = \begin{pmatrix} .80 & .10 & .10 \\ .05 & .80 &.15 \\ .00 & .00 & 1.0 \end{pmatrix} \]

Assim, temos os seguintes fluxos brutos esperados:

\[ M = \begin{pmatrix} \mu_{ij} \end{pmatrix} = \begin{pmatrix} 68000 & 8500 & 8500 \\ 500 & 8000 & 1500 \\ 0 & 0 & 5000 \end{pmatrix} \]

Esta população, no entanto, é não-observável: por causa da não-resposta, algumas observações perdem as suas categorias. As probabilidades de responder no período inicial são \(\phi ( i ) = ( .95 , .40 , .80 )\) para os indivíduos classificados como “S”, “I”, e “R”, respectivamente. A probabilidade de responder no período final dado que respondeu no período inicial é \(\rho_{RR} = .9\). Já os indivíduos que não responderam no período inicial tem probabilidade de não-resposta igual à \(\rho_{MM} = .7\). Esta é população com não-resposta é chamada de população observável.

Desta população observável, selecionamos uma amostra aleatória simples de tamanho \(n =5000\).

O analista ingênuo pode supor que a não-resposta é aleatória e, portanto, estima as probabilidades descartando as observações com não-resposta. Ele obtêm a seguinte matriz de fluxos:

\[ \widehat{M}_{MCAR} = \begin{pmatrix} 71389 & 10058 & 9352 \\ 227 & 3327 & 706 \\ 0 & 0 & 4941 \end{pmatrix} \]

Comparando as duas matrizes, é possível suspeitar que existe viés. Por exemplo, a estimativa do fluxo Infectados-Infectados subestima o fluxo bruto esperado em 58%.

No entanto, um pesquisador mais experiente reconhece que existe um padrão de não-resposta diferencial. Usando o modelo que considera o mecanismo de não-resposta, ele obtém a seguinte matriz

\[ \widehat{M}_{Modelo} = \begin{pmatrix} 66659 & 9392 & 8733 \\ 538 & 7888 & 1673 \\ 0 & 0 & 5117 \\ \end{pmatrix} \]

Magicamente, o viés desta estimativa cai para aproximadamente 1%!

Outra consequência importante dessa correção é que as estimativas dos fluxos líquidos também mudam. Supondo que a não resposta é ignorável, teríamos \(\widehat{\eta}_{MCAR} = \begin{pmatrix} .91 & .04 & .05 \end{pmatrix}\), enquanto \(\widehat{\eta}_{Modelo} = \begin{pmatrix} .85 & .10 & .05 \end{pmatrix}\). Consequentemente, a distribuição final também muda. Os valores dos parâmetros associados às probabilidades finais são \(\kappa = \begin{pmatrix} .685 & .165 & .150 \end{pmatrix}\). Enquanto a estimativa ingênua resulta em \(\widehat{\kappa}_{MCAR} = \begin{pmatrix} .716 & .134 & .150 \end{pmatrix}\), enquanto \(\widehat{\kappa}_{Modelo} = \begin{pmatrix} .672 & .173 & .155 \end{pmatrix}\). Ou seja: as estimativas das margens também são corrigidas, ficando mais próximas dos valores esperados.

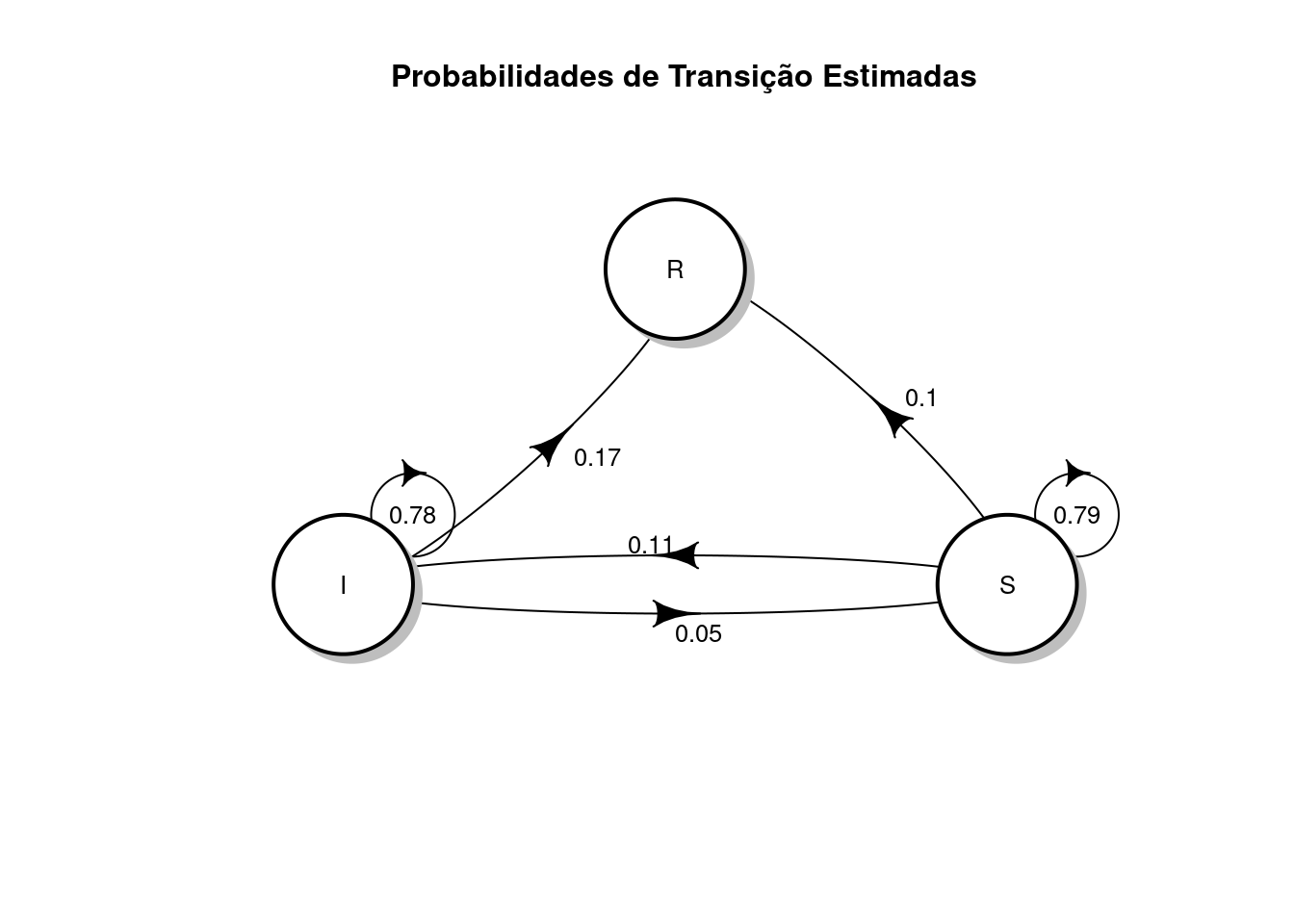
As probabilidades de transição podem ser representadas usando diagramas de fluxo, como na figura abaixo. À primeira vista, este diagrama pode ser um pouco complicado, mas, na verdade, é bastante simples. Observe o o círculo com a letra “I”. Ele representa o fluxo de pessoas infectadas. As setas saindo do círculo I são os probabilidades de saída, enquanto às setas apontando para ele são probabilidades de permanência. Assim, 17% das pessoas infectadas se recuperaram, 5% voltaram a ser suscetíveis à doença, e 78% continuaram infectados.