ENEM e desigualdade na educação: uma análise dos dados de 2015
Há alguns dias atrás, rolou o ENEM desse ano. E daí veio a ideia para este post: analisar a desigualdade na educação entre os jovens do Ensino Médio a partir das pontuações dos candidatos. Usando R, como sempre.
Vou tentar manter as complicações matemáticas fora da questão e focar na aplicação da técnica para entender o contexto da desigualdade educacional. Assim, pretendo trazer gente de outras áreas, como pedagogos e sociólogos, que podem se beneficiar de mais uma ferramenta para analisar o problema, além de contribuir com novas perspectivas para “aqueles que só pensam com números”1.
E, sim, hoje vai ser tudo em português.
Pegue seu café, sente-se confortavelmente e vamos lá!
ENEM
O Exame Nacional do Ensino Médio (ENEM) é uma prova realizada anualmente pelo Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (INEP), um órgão associado ao Ministério da Educação. A finalidade do ENEM é avaliar a qualidade do ensino médio e, desde 2009, tornou-se a principal forma de ingresso nas universidades públicas do Brasil. De fato, esse é o segundo maior vestibular do mundo, ficando atrás apenas do exame de admissão chinês.
Embora a prova exista desde 1998, foi com o estabelecimento do SiSU que o número de examinados cresceu. Assim, o exame, antes composto majoritariamente por estudantes de escolas públicas, passou a ser amplamente utilizada pelos de escolas particulares. Essa mudança proporciona um experimento interessante sobre o desempenho dos estudantes do Brasil.
Desigualdade e educação
Essa parte contém um pouco de matemática.
Mas, não se assuste: vou tentar explicar tudo sem muita complicação.
O estudo da desigualdade é uma mistura de economia, filosofia, matemática e estatística. Embora os estudos neste campo se voltem majoritariamente às distribuições de renda e riqueza, existem vários trabalhos discutindo outras formas de desigualdade.
No entanto, o tipo de variável costuma ser o principal desafio: renda é uma variável contínua, enquanto o estado de saúde, por exemplo, costuma ser uma variável ordinal. Esse tipo de problema é comum na análise de aspectos qualitativos do bem-estar. Em outras palavras, quando perguntadas a respeito de sua saúde, as pessoas não respondem “estou com 75 de saúde” a não ser que você esteja jogando LOL ou algo do tipo, mas algo como “ruim” , “bem”, “excelente”. Quando temos esse tipo de resposta, não dá pra simplesmente calcular um índice de Gini. Caso você se interesse por esses problemas, Cowell e Flachaire (2017) é uma leitura obrigatória, mostrando como as medidas tradicionais falham e propondo uma classe de medidas que atende os axiomas propostos.
Dito isso, cabe a pergunta: existe uma medida cardinal da desigualdade em educação? Se considerarmos o desempenho dos alunos em provas, pode-se dizer que sim. A lógica é mais ou menos essa: quanto mais preparado o aluno, melhor o desempenho na prova. Se o desempenho é medido em pontuação e não em categorias, podemos usar a pontuação para medir a desigualdade.
Evidentemente, essa abordagem tem seus problemas, desde provas mal formuladas a seleção de alunos examinados. Esse último é particularmente sério. Como a média das notas de uma escola é tomada como uma indicação da qualidade do seu ensino, um diretor mais mal intencionado pode dificultar a candidatura dos alunos que teriam uma pontuação ruim. Desta forma, a amostra se torna viesada. Isso é mais possível em escolas particulares, já que é mais provável que os alunos tenham condições financeiras de ir para uma faculdade particular.
A própria percepção do diferencial de desempenho entre escolas públicas e particulares pode ser causar um viés na amostra. O aluno que pensa não ter chance no vestibular não tem muito incentivo para fazer a prova. Existe uma miríade de aspectos socioeconômicos que fazem com que esse comportamento ocorra.
Com essas ressalvas em mente, prossigamos.
Algumas estatísticas sobre o ENEM 2015
Para entender um pouco de como se distribuem resultados, vamos analisar quem são os 1000 melhores e os 1000 piores de acordo com o desempenho nas provas. No exercício a seguir, analisaremos apenas os dados dos alunos que:
- Estavam concluindo o ensino médio em 2015, e
- Estiveram presentes em todas as provas, e
- Não tiveram qualquer problema na redação, e
- Não estavam fazendo a prova apenas para medir seus conhecimentos.
Em outras palavras: estamos trabalhando com a interseção destes quatro conjuntos de examinados, não a união.
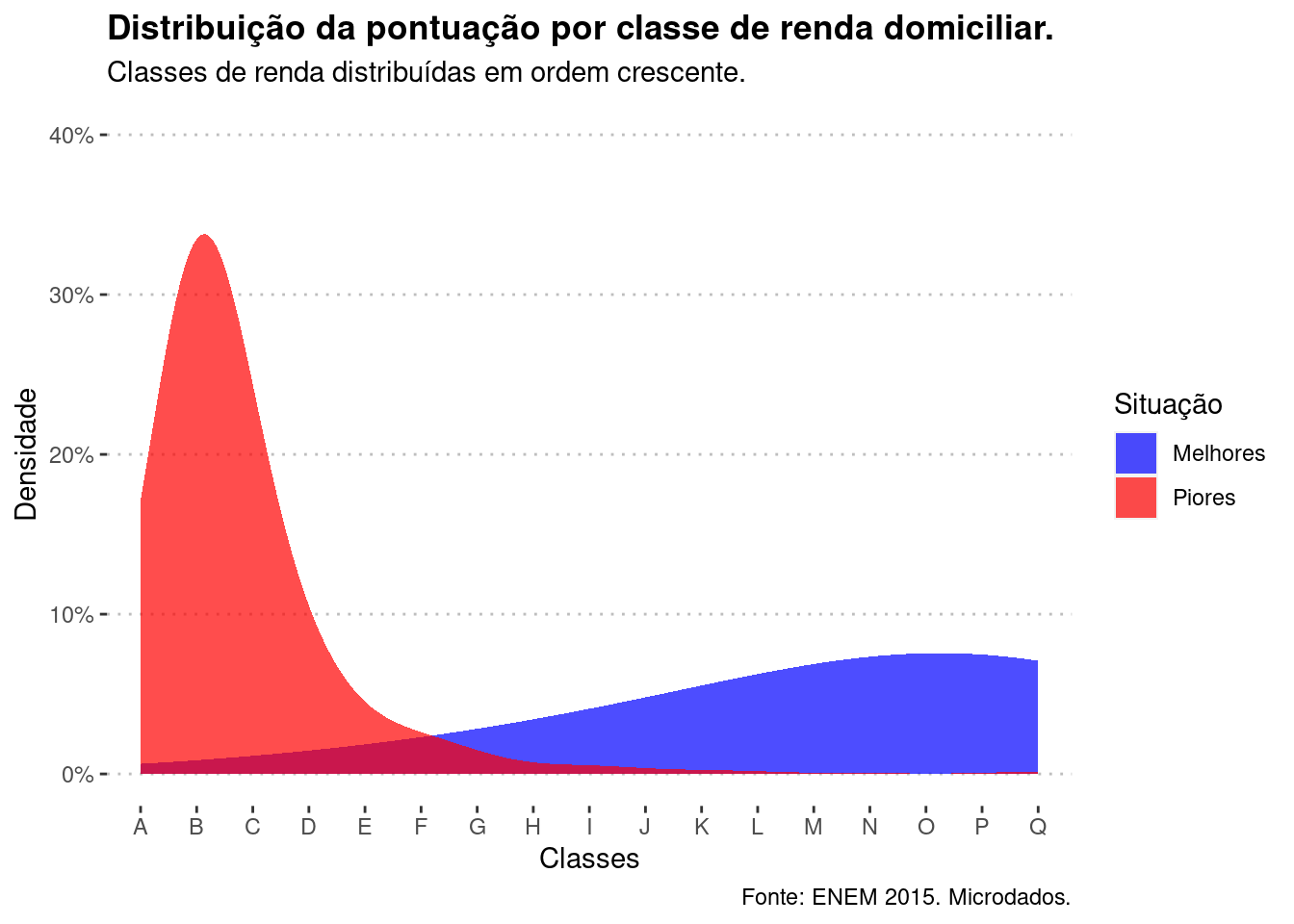
O gráfico \(\ref{dist_extreme}\) abaixo mostra como as notas dos extremos se distribuem. Enquanto os melhores desempenhos tendem a se concentrar mais entre domicílios mais ricos, os piores desempenhos se concentram ainda mais entre os domicílios mais pobres. Ou seja, é bem mais provável que uma “nota baixa” venha de um domicílio de baixa renda. O “monte” em vermelho entre os domicílios de catagoria “B” e “C” mostra isso. E a queda se comparado a categoria “A” se deve principalmente a raridade destes indivíduos, seja porque realmente existem poucos domicílios com nenhuma renda, seja porque as pessoas destes domicílios tendem a não fazer a prova.
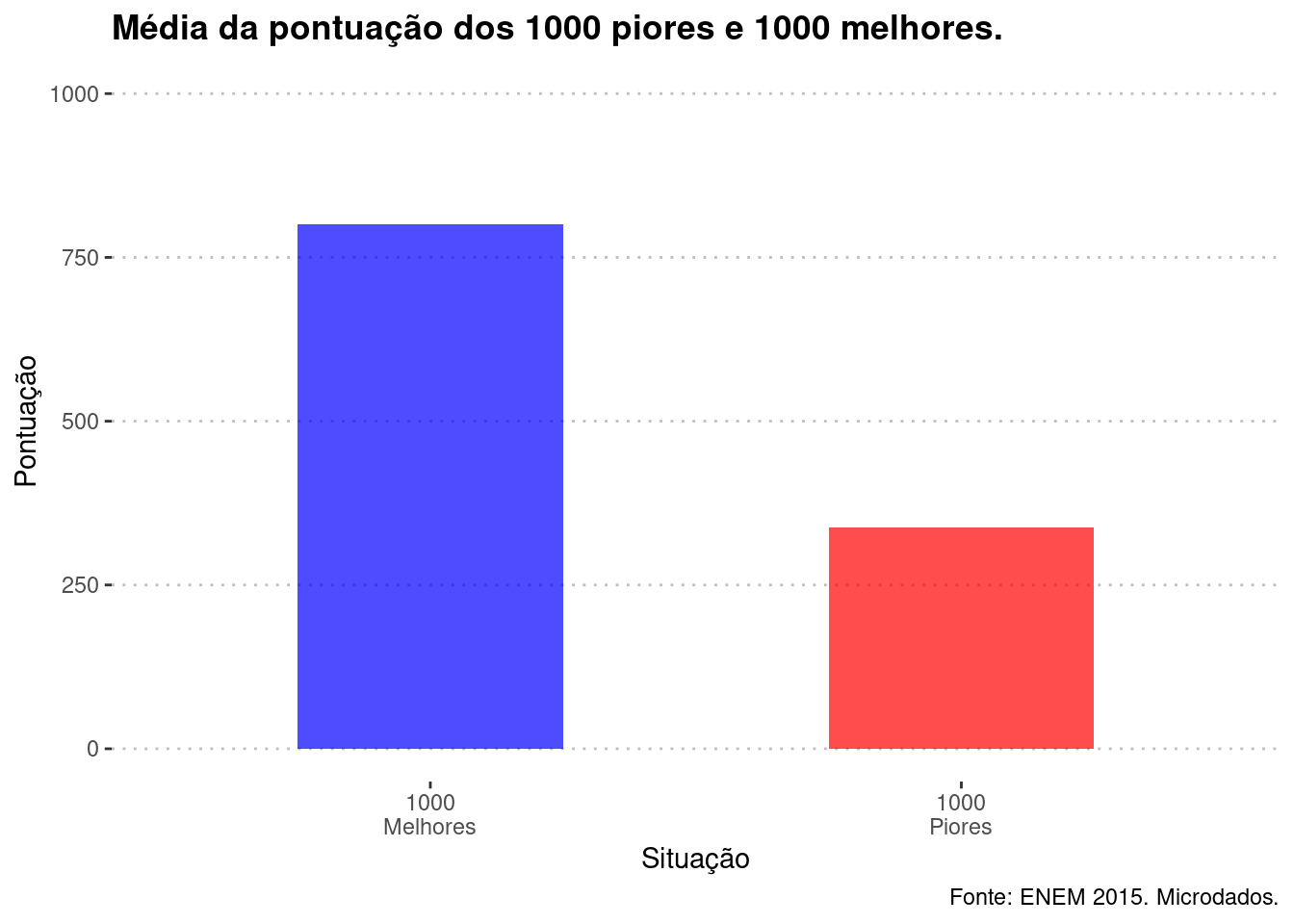
Ok, mas e as médias? A média da pontuação dos extremos é bem diferente, como de se esperar. De fato, a pontuação dos melhores é aproximadamente 2.7 vezes melhor que a dos piores. O gráfico \(\ref{avg_extreme}\) abaixo mostra esta discrepâncias.
Como medir: um exercício de decomposição por subgrupos.
Se você já leu alguma coisa sobre desigualdade, você deve ter visto estimativas do índice de Gini. Essa é, de longe, a medida de desigualdade mais conhecida. Mas também existem outras medidas bem interessantes. Uma medida recente é a J-divergência, proposta por Rohde (2016). Ela tem uma vantagem sobre o índice de Gini: decomposição por subgrupos. I.e., a estimativa pode mostrar o quanto se deve a desigualdade entre grupos e intra-grupos.
As duas medidas estão disponíveis no pacote convey (Pessoa, Damico e Jacob, 2017a), incluindo a decomposição da J-divergência. Facilmente encontradas em Pessoa, Damico e Jacob (2017b), as fórmulas dos indicadores são essas:
\[ \begin{aligned} G &= 1 - 2 \int_{0}^{1} L(p)dp \\ J &= \int_{0}^{\infty} \bigg( \frac{ y_i - \mu }{ \mu } \bigg) \log \bigg( \frac{y_i}{\mu} \bigg) f \big( y_i \big) dy \end{aligned} \] onde \(L(\cdot)\) é a curva de Lorenz.
Nota: talvez eu devesse parar com o marketing pessoal.
Na prática
Vamos usar os dados do ENEM 2015, disponíveis na página de microdados do INEP. Depois de colocar os dados numa base MonetDB, vou criar um “pseudo-desenho amostral”. Por que “pseudo”? Porque a base não é uma amostra propriamente dita. Então, por que fazer isso? As funções do convey só funcionam sobre objetos de desenho amostral. Além disso, o convey funciona bem com bases de dados externas, usando apenas as informações necessárias para o cálculo.
| Área | Gini | J-divergência |
|---|---|---|
| Brasil | 0.0822 | 0.0211 |
| Norte | 0.0765 | 0.0186 |
| Nordeste | 0.0834 | 0.0220 |
| Sudeste | 0.0808 | 0.0203 |
| Sul | 0.0740 | 0.0171 |
| Centro-Oeste | 0.0809 | 0.0207 |
As primeiras coisas que percebemos ao olhar a tabela \(\ref{tabela1}\) são: (1) existe menos desigualdade nesta distribuição do que em distribuições de renda, e (2) o índice de Gini é maior que a J-divergência. A primeira observação decorre de um aspecto um tanto óbvio: as pontuações tem um limite superior, ao contrário das distribuições de renda. Em outras palavras, uma pessoa não pode ter mais do que 1 000 pontos, embora sua renda pode extrapolar esse limite. O segundo aspecto também é interessante: o índice de Gini é mais sensível às desigualdades próximas da média, enquanto a J-divergência tende a ser mais sensível às desigualdades nas caudas. Consequentemente, podemos supor que a maior parte da desigualdade está no meio da distribuição.
É normal que a diferença entre categorias apresente um valor menor que a desigualdade dentro das categorias, mesmo para renda. Dito isso, a decomposição da J-divergência, na tabela \(\ref{tabela2}\) abaixo, mostra alguns padrões interessantes. Apesar de todo retrocesso recente, A desigualdade no desempenho entre os gêneros2 praticamente não se deve a este aspecto. A decomposição captou impactos das diferenças entre cor/raça, embora esses sejam menores que os impactos decorrentes do tipo de escola3 ou da renda. No caso da renda, 30% da desigualdade pode ser atribuída à desigualdade entre as classes.
| J-divergência | Entre | Intra | |
|---|---|---|---|
| Gênero | 0.0211 | 0.0211 | 0.0001 |
| Cor/Raça | 0.0211 | 0.0199 | 0.0013 |
| Tipo de Escola | 0.0211 | 0.0154 | 0.0058 |
| Renda | 0.0211 | 0.0152 | 0.0060 |
Concluindo
Com esse exercício, quis mostrar que, embora os indicadores de desigualdade sejam normalmente associados às distribuições de renda, eles podem ser aplicados a outras distribuições. No caso, eles podem ajudar a entender aspectos da desigualdade na educação, desde que aplicados corretamente.
No entanto, o problema da desigualdade com variáveis ordinais continua aberto. Ainda não existem muitos trabalhos a respeito de inferência estatística com este tipo de medida. Deixo aqui uma possível cena dos próximos capítulos: será que podemos calcular desigualdade em saúde usando a Pesquisa Nacional de Saúde levando em consideração o desenho amostral complexo?
Peut être.
