A identidade fundamental de Meng (2018)

Vamos partir do problema colocado em Meng (2018, p. 689).

Considere uma população com \(N\) indivíduos rotulados \(j \in J, J = \{ 1, \dots , N \}\). Os \(p\) atributos destes indivíduos são registrados numa matriz \(\mathbf{X}\) de dimensão \(N \times p\). Suponha que você queira estudar a média do atributo \(G \in \mathbf{X}\) na população, dada por \(\overline{G}_N\). Dispomos, no entanto, da amostra \(I_n \subset \{ 1, \dots , N \}\) de tamanho \(n\) dos indivíduos da população. Vamos estimar a média populacional a partir do estimador da média amostral, definido abaixo:

\[ \overline{G}_n = \cfrac{ \sum_{j \in I_n} G_j }{ n } = \cfrac{ \sum_{j \in J} R_j G_j }{ \sum_{j \in J} R_j } . \] onde \(R_j\) é uma variável indicadora que representa a presença do indivíduo \(j\) na amostra \(I_n\). Como diz Meng (2018, p. 689), a variável \(R_j\) representa o mecanismo de registro através do qual obtemos a amostra \(I_n\). O viés deste estimador é dado por:

\[ \begin{aligned} \overline{G}_n - \overline{G}_N &= \cfrac{ \sum_{j \in U} R_j G_j }{ \sum_{j \in U} R_j } - \cfrac{ \sum_{j \in U} G_j }{ N } = \cfrac{ \sum_{j \in U} R_j G_j }{ N } \bigg( \cfrac{ \sum_{j \in U} R_j }{ N } \bigg)^{-1} - \cfrac{ \sum_{j \in U} G_j }{ N } \\ &= \cfrac{ E_J \big( R_J G_J \big) }{ E_J \big( R_J \big) } - E_J \big( G_J \big) \\ &= \cfrac{ E_J \big( R_J G_J \big) - E_J \big( R_J \big) E_J \big( G_J \big) }{ E_J \big( R_J \big) } \\ &= \cfrac{ Cov \big( R_J , G_J \big) }{ E_J \big( R_J \big) } \end{aligned} \] e o fato de que \(E_J ( R_J ) = n / N = f\), onde \(f\) é a fração amostral de \(I_n\), cuja variância é \(\sigma^2_R = f ( 1 - f)\). Usando estas informações e a fórmula da correlação, temos: \[ \begin{aligned} \overline{G}_n - \overline{G}_N &= \cfrac{ Cov \big( R_J , G_J \big) }{ E_J \big( R_J \big) } = \rho_{R,G} \times \cfrac{ \sigma_R }{ f } \times \sigma_G \\ &= \rho_{R,G} \times \sqrt{ \cfrac{ 1 - f }{ f } } \times \sigma_G. \\ \end{aligned} \]

Esta última identidade é importantíssima. Ela mostra que o viés é um produto de três componentes: (1) a correlação entre o mecanismo de resposta e a variável estudada, indicando a qualidade dos dados; (2) uma relação sobre a fração amostral, indicando o tamanho dos dados; e (3) o desvio-padrão de \(G\), que indica a dificuldade do problema de estimação.

Sob a hipótese de ausência de viés de não-resposta, o Erro Quadrático Médio de \(\overline{G}_n\) é dado por: \[ \begin{aligned} EQM \big( \overline{G}_n \big) &= \rho^2_{R,G} \times { \cfrac{ 1 - f }{ f } } \times \sigma^2_G = D_I \times D_O \times D_U, \end{aligned} \] onde \(D_I\) é o que Meng chama de Data Defect Index. Meng (2018) explora vários detalhes e insights desta fórmula, mas vamos manter o foco na nossa pergunta principal: escolher uma amostra probabilística de 5% da população ou uma amostra não-probabilística de 80% da população?

Comparando Amostras Aleatórias Simples (AAS) e Amostras Não-Probabilísticas (ANP)

No caso de uma AAS, o estimador \(EQM_{AAS} \big( \overline{G}_n \big)\) é igual a variância do respectivo estimador da média. Assim, \[ \begin{aligned} &\frac{1-f}{n} \cfrac{N}{N-1} \sigma^2_G = D_I \times { \cfrac{ 1 - f }{ f } } \times \sigma^2_G \\ & \therefore D_I^{AAS} = \cfrac{1}{N-1}. \end{aligned} \] Ou seja: sob AAS, o \(D_I\) desaparece muito rápido. Por exemplo, se a população tem tamanho 11, teríamos \(D_I^{AAS} = 1/10\). Para uma população de tamanho 1001, , teríamos \(D_I^{AAS} = 0,001\).

Para ajudar a entender o impacto comparativo disso, Meng (2018) propõe uma medida do “Efeito do Plano Amostral” (EPA) para . Coloco entre aspas porque, embora ela se pareça o EPA da teoria de amostragem, tem uma diferença importante: no contexto de amostragem, estamos comparando variâncias de planos amostrais alternativos em relação ao plano AAS; neste caso, estamos comparando o EQM de estimativas baseadas em um plano não probabilístico com a variância do plano AAS. Então, considerando \(D_O\) e \(D_U\) fixos, temos:

\[ \begin{aligned} EPA = \cfrac{ E_R \big[ \overline{G}_n - \overline{G}_N ]^2 }{ Var_{AAS} ( G_n ) } = (N - 1) D_I. \end{aligned} \] A interpretação dela é a seguinte: considerando os mesmos estimadores, \(D_O\) e \(D_U\), o EQM de uma ANP é (EPA) vezes a variância do mesmo estimador se essa amostra fosse AAS. Perceba que ele cresce com o tamanho da população e com \(D_I\).

Big data versus Amostras Probabilísticas

A vantagem de registros administrativos e big data é o tamanho da sua cobertura. Precisamos fazer uma comparação mais realista. Passamos, então, a considerar os casos quando os \(f\) são diferentes.

Meng (2018, p. 698) aplica o seguinte procedimento: iguala-se o EQM com a respectiva variância sob AAS. Vou usar um resultado diferente, mas que serve para mostrar a mesma ideia²:

\[ D_O^{AAS} = (N - 1) D_I \times D_O^{ANP} \\ f_{AAS} = \cfrac{1}{ (N - 1) ( 1/f_{ANP} - 1) D_I + 1 }. \]

Esta fórmula mostra o quanto seria a fração amostral sob AAS para uma dada fração amostral ANP. Veja que \(f_{AAS}\) também depende de \(D_I\) e de \(N\), o tamanho da população. Usando este resultado, vamos explorar alguns casos.

Caso 1: \(D_I = 0.001\)

A Figura 1 mostra o impacto dramático que \(D_I = 0.001\), um valor que parece bem pequeno, tem sobre as ANPs. Por exemplo, tomemos uma ANP que cobre 80% da população. Em uma população de 100 000 indivíduos, uma AAS de 5% já é melhor do essa ANP. Em uma população de 1 000 000 indivíduos, uma AAS de 0.4% da população já é melhor que esta ANP!

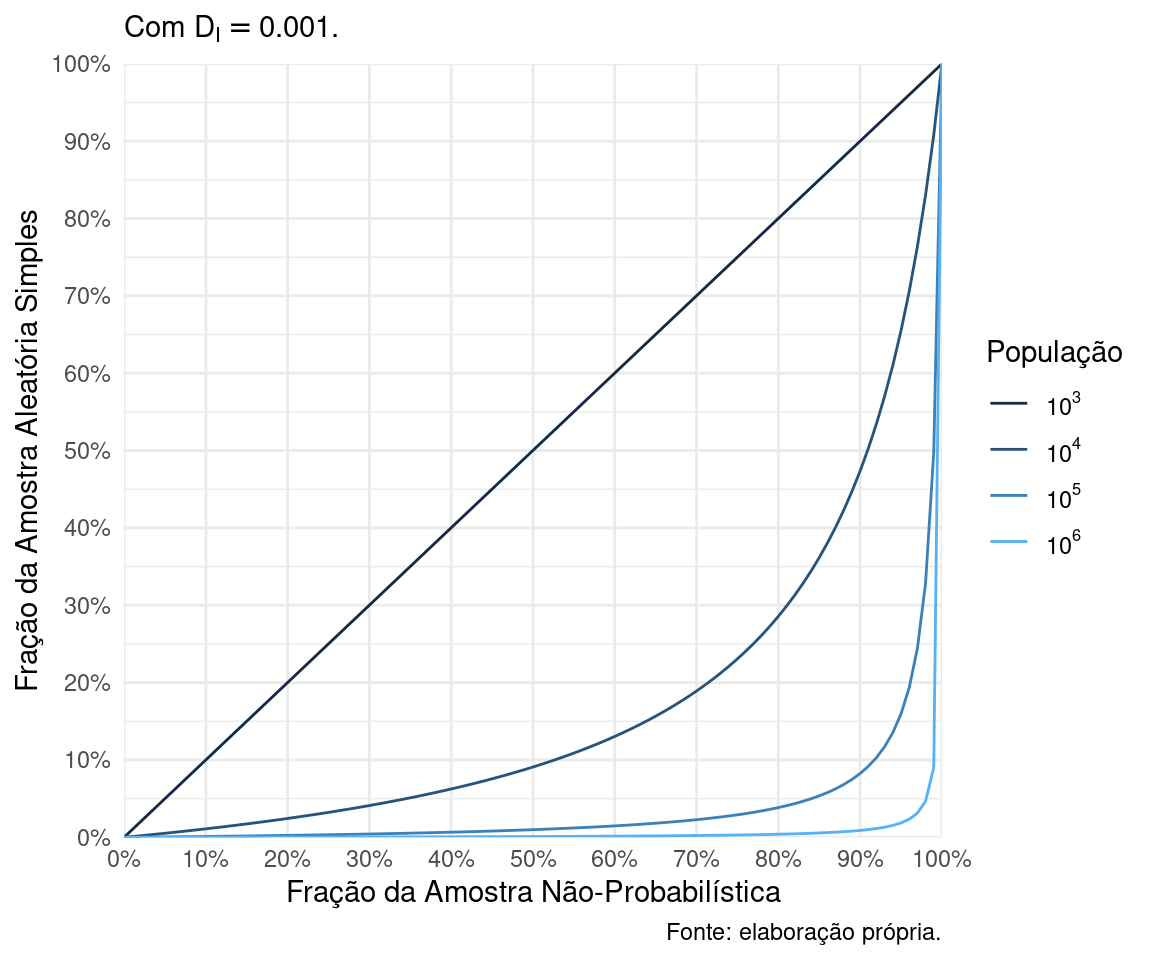
Figure 1: Equivalência entre AAS e ANP para populações de diferentes tamanhos.

Caso 2: \(N =\) 200 milhões

Vamos considerar uma população com aproximadamente o mesmo tamanho da população brasileira. A Figura 2 mostra a equivalência entre as frações amostrais neste caso, variando apenas \(D_I\).

Não, o gráfico não está errado: para esses \(D_I\), o gráfico só é legível quando limitamos as frações AAS equivalentes menores que 1%! Para \(D_I = 10^{-6} = 0.000001\), um valor ínfimo, uma AAS de 0.75% da população é equivalente a uma ANP de 60%. Com \(D_I = 10^{-5} = 0.00001\), uma AAS de 0.45% da população é melhor que uma ANP de 90%. Com \(D_I = 10^{-4} = 0.0001\), uma ANP que cobre 99% da população tão boa quanto uma AAS de aproximadamente 0.5% da população!

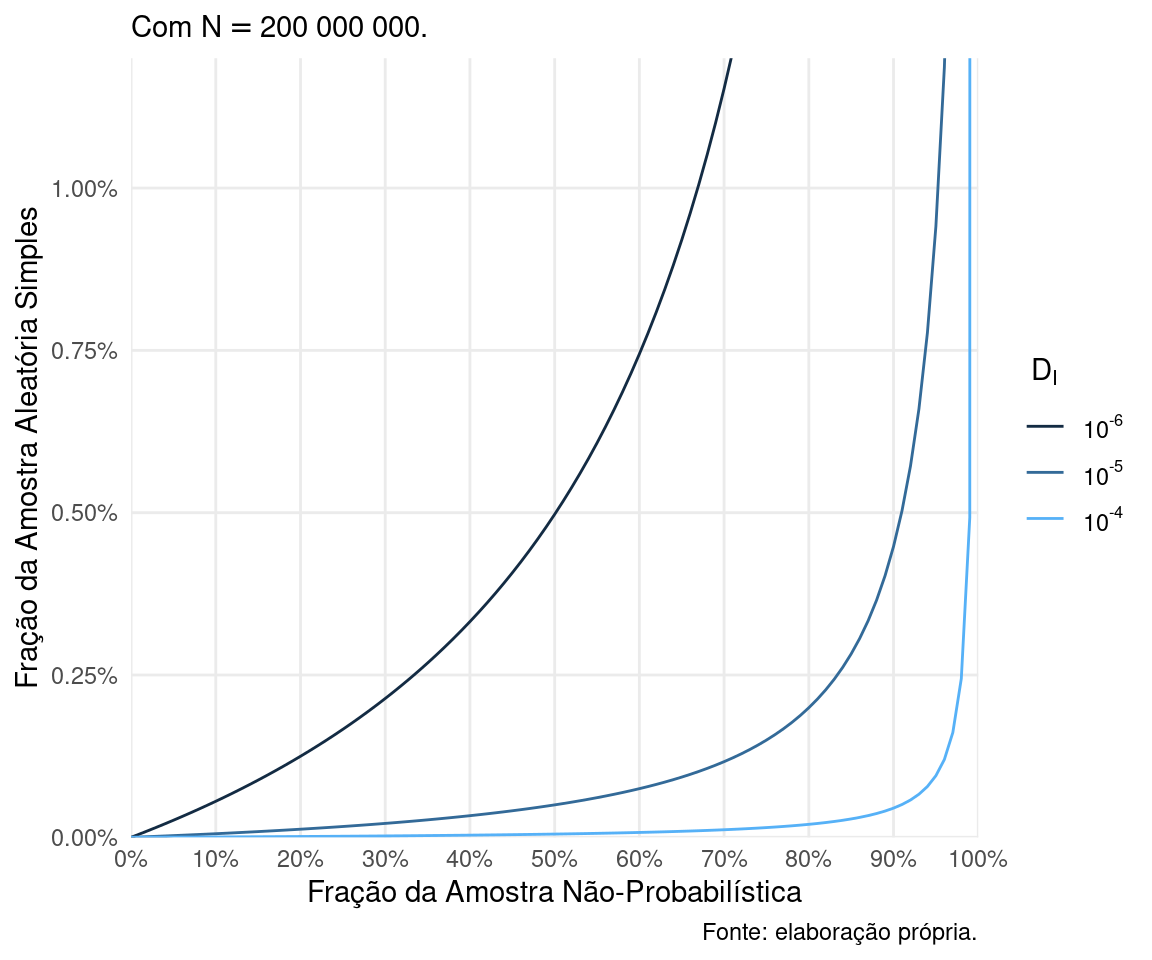
Figure 2: Equivalência entre AAS e ANP para uma população de 200 milhões de indivíduos.

Comentários finais

Skinner e Wakefield alertam:

[…] Há também um enorme interesse atual na avalanche de novas técnicas de análise de dados, que frequentemente têm suas origens em machine learning. No entanto, embora muitos desses métodos pareçam inebriantes, eles devem ser avaliados cuidadosamente em face das múltiplas fontes de não-cobertura e seleção. Se tais aspectos forem ignorados, existe uma possibilidade genuína que análises de big data produzirão grandes desastres inferenciais. (Skinner e Wakefield, 2017, p. 174, grifo nosso)

Meng (2018) mostra que este alerta se estende para técnicas “menos moderninhas”, como é o caso de uma média simples. Mas nem tudo é má notícia para as ANPs. Sob a hipótese de ausência de não-resposta, o viés na análise é explicado pelo \(D_I\), um componente associado à auto-seleção/qualidade da cobertura da ANP. Entretanto, na prática, não temos como calcular o \(D_I\). Kalton (2019, p. S25) aponta que “[o] valor de uma grande ANP pode ser maior para estimativas analíticas, cujos vieses podem ser menores, e para pequenos grupos que não podem ser amostrados eficientemente com os métodos padrões baseados no desenho”. Kim e Wang (2019) propõem duas técnicas para reduzir o viés de seleção: amostragem inversa e survey data integration. Elliott e Valliant (2017) exploram abordagens baseadas em quasi-aleatorização e modelos de superpopulação. Sen et al. (2019) propõem um quadro conceitual análogo ao Total Survey Error para ajudar a entender as limitações e possibilidades do big data, que também se aplica para ANPs em geral. Mas isso é tema para outro post.

O ponto central deste artigo é que, para estatística oficial, se os seus sistemas de registro administrativo não forem excelentes, uma amostra probabilística é muito melhor.