Quebrando o TCL para Populações Finitas sob Amostragem Sem Reposição
Aviso: Esse exemplo é discutido na aula sobre Métodos de Monte Carlo em Populações Finitas, elaborada ao longo do meu estágio de docência em Estatística Computacional 2.
Um dos resultados teóricos com maior resultado prático é o Teorema Central do Limite. Ele fundamenta a aproximação da distribuição (assintótica) de um estimador pela distribuição normal, sendo a base da construção dos intervalos de confiança “tradicionais”. Em linhas gerais, a interpretação usual é que quanto maior \(n\) — o tamanho da amostra —, melhor é a aproximação pela distribuição normal.
Não é difícil encontrar simulações mostrando aplicações deste teorema, mas vamos fazer algumas no contexto de populações finitas.
Primeiro, vamos simular a nossa população finita. Vamos considerar uma população de tamanho \(N = 5000\) com três variáveis: \(y_1\), \(y_2\) e \(y_3\).
## y1 y2 y3
## Min. : 53.83 Min. :102.5 Min. :-38.89
## 1st Qu.:106.79 1st Qu.:110.7 1st Qu.: 62.60
## Median :120.55 Median :120.2 Median : 80.18
## Mean :120.29 Mean :127.5 Mean : 73.17
## 3rd Qu.:133.90 3rd Qu.:138.0 3rd Qu.: 89.30
## Max. :190.40 Max. :250.2 Max. : 97.41A distribuição das variáveis na população podem ser visualizadas na Figura 1. A distribuição de y1 é simétrica, enquanto as distribuição de y2 e y3 são assimétricas. Isso vai ser importante em breve.
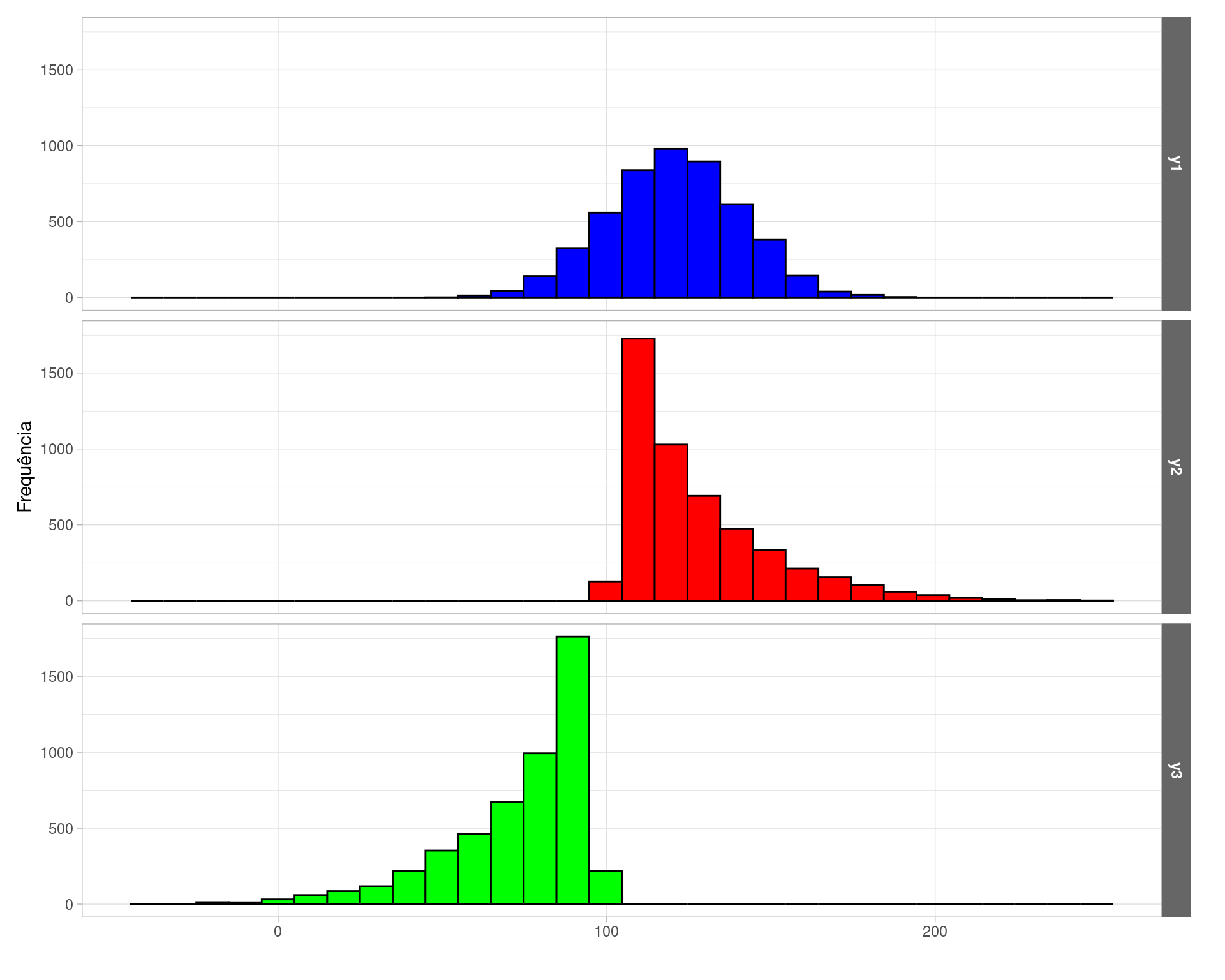
Figure 1: Distribuição das variáveis na população.
Distribuição da Média Amostral sob Amostragem Aleatória Simples Com Reposição
Para estudar a distribuição da média amostral, vamos extrair SIM = 10^4 amostras simples com reposição com tamanhos diferentes. Para cada uma destas amostras, calculamos a média amostral das variáveis de interesse. Para analisar a distribuição, usaremos a distribuição padronizada do estimador da média:
\[ z_s = \frac{ \overline{y}_s - \overline{Y}}{\text{Var}_p [ \overline{y}] } \]
onde \(\overline{y}_s\) é a média amostral da amostra \(s\), \(\overline{Y}\) é a média populacional e \(\text{Var}_p [ \overline{y}]\) é a variância do estimador média amostral sob o plano amostral (neste caso, AASC).
A Figura 2 mostra que a distribuição do estimador média amostral se aproxima de uma distribuição normal, conforme prevê o TCL.
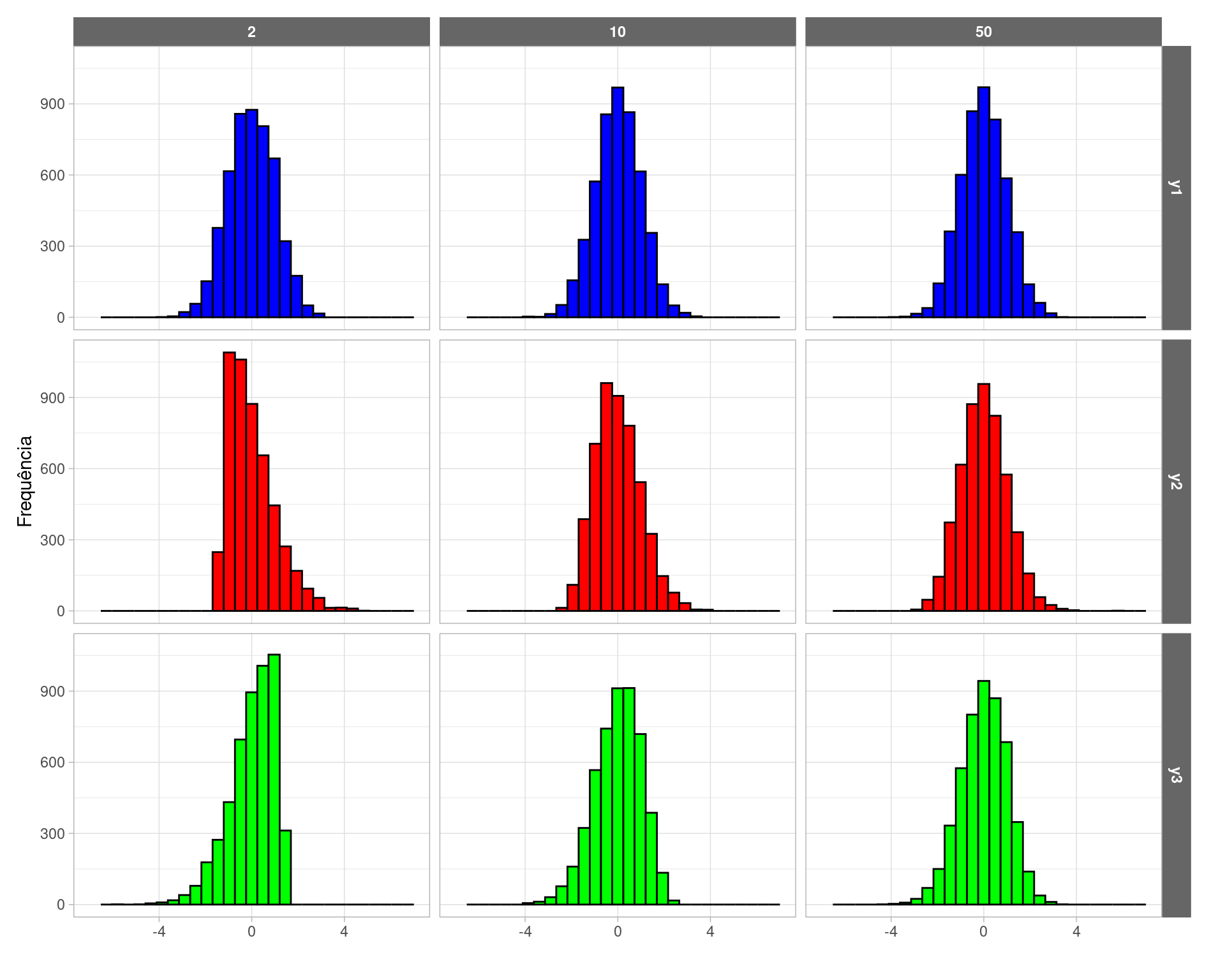
Figure 2: Distribuição das médias amostrais padronizadas sob AASC
Distribuição da Média Amostral sob Amostragem Aleatória Simples Sem Reposição
A Figura 3 mostra que a distribuição do estimador média amostral se aproxima de uma distribuição normal, conforme prevê o TCL. Bastante similar à Figura 2, inclusive.
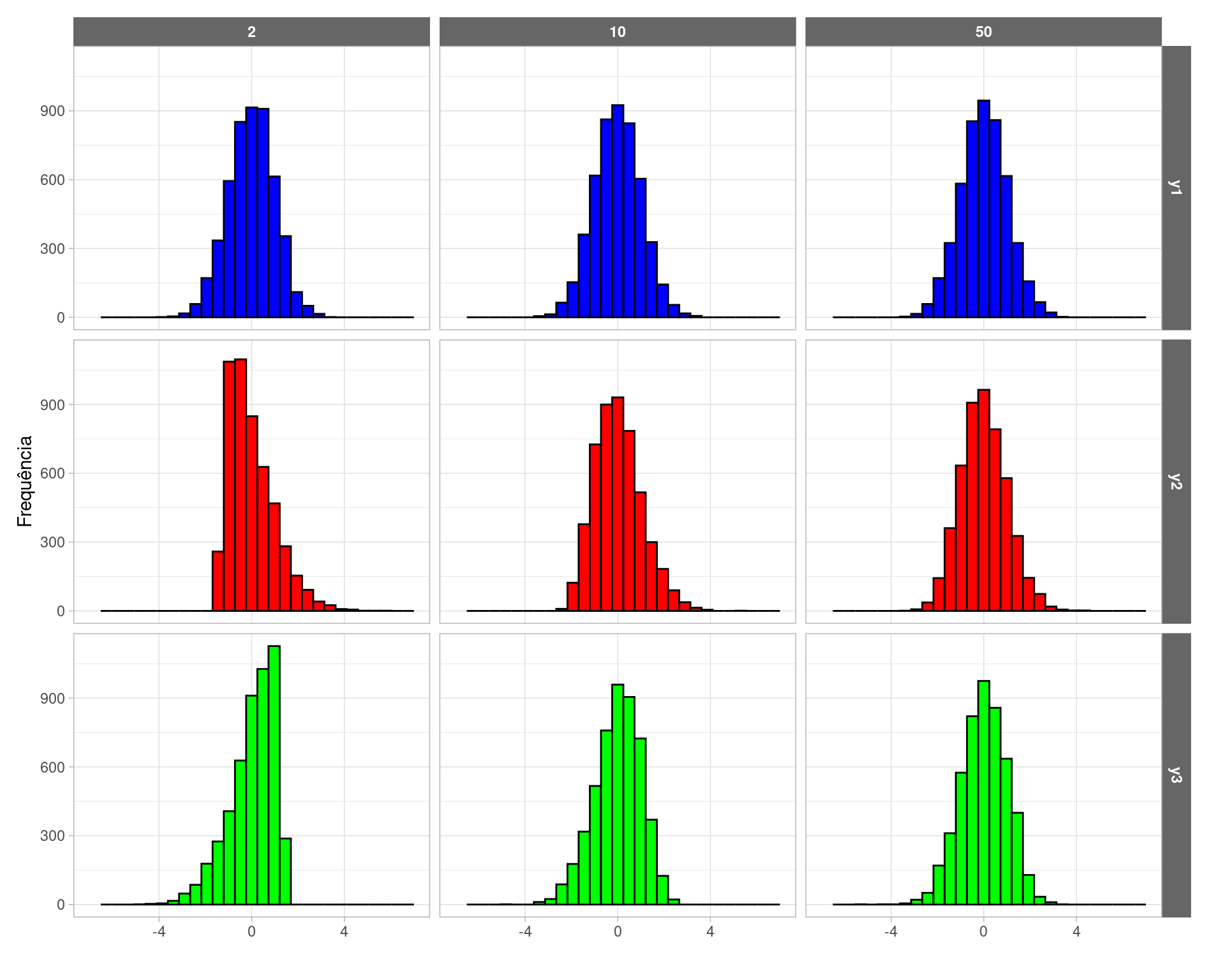
Figure 3: Distribuição das médias amostrais padronizadas sob AAS
Tudo funcionando de acordo com o TCL. Mas o que acontece quando fazemos o tamanho da amostra ser muito grande em relação à população finita? A Figura 4 mostra que a aproximação pela distribuição normal piora quando \(n\) é muito grande!
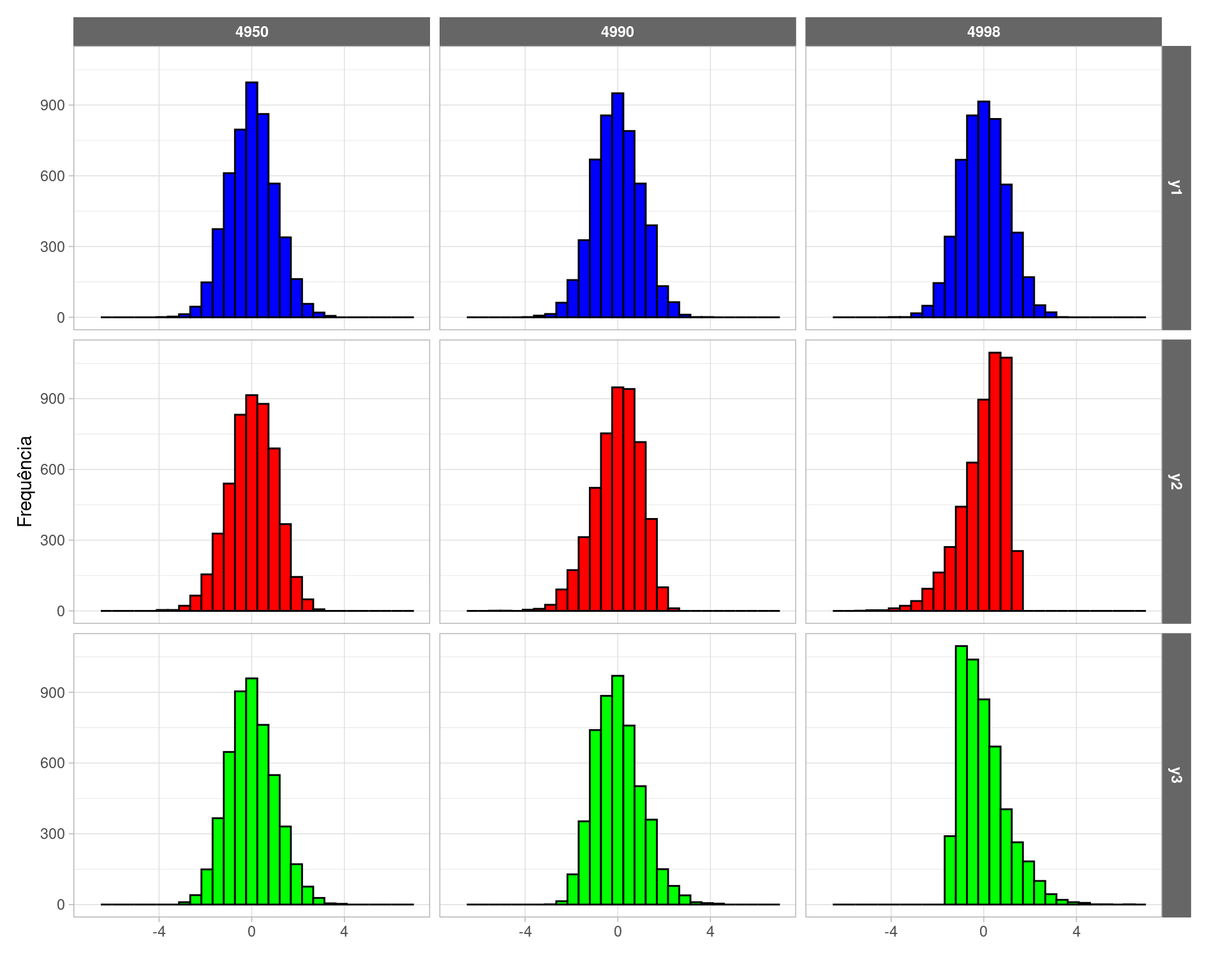
Figure 4: Distribuição das médias amostrais padronizadas sob AAS
Na teoria de amostragem, este tipo de paradoxo já foi bastante discutido. Existe uma maneira de desenvolver resultados assintóticos, mas ela exige que \(N\) e \(n\) tendam ao infinito. Este contra-exemplo foi apresentado originalmente por Plane e Gordon (1982).
